【電験二種（理論）＜R４：問４＞】過去問解説！〜過渡現象をラプラス変換で解く〜

過去問【電験二種（理論）＜R４：問４＞】過渡現象をラプラス変換で解いていきます。

※参考文献は以下の通りです。

問題【電験二種（理論）＜R４：問４＞】

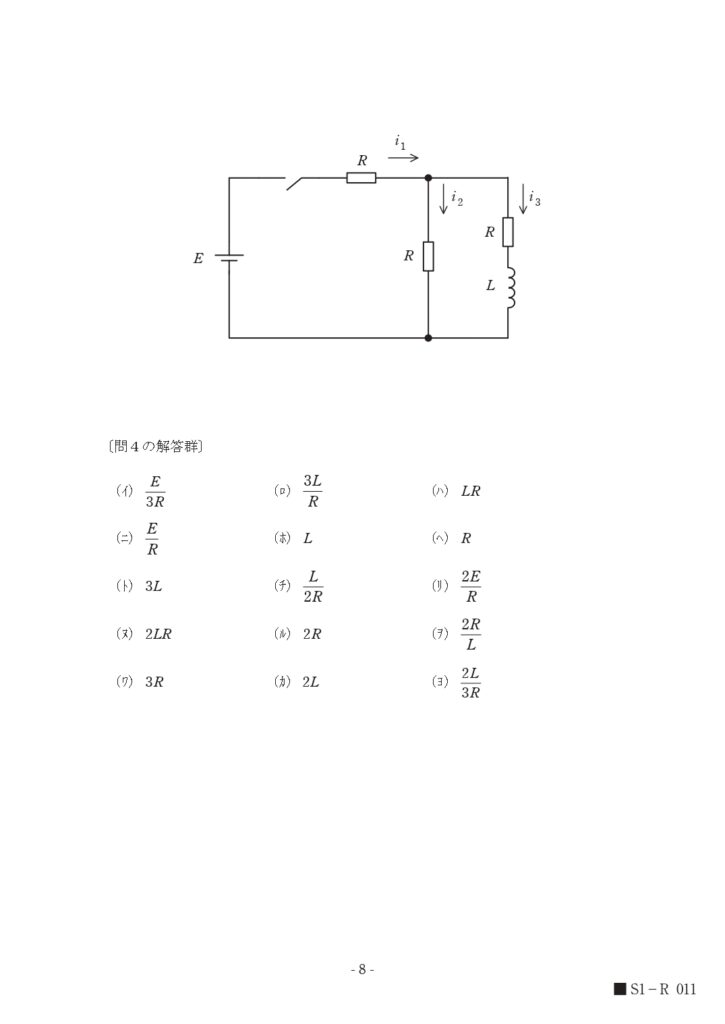
解説

(1),(2)の回答

題意より、③式に①式を代入すると

\(E=R(i_{ 2 }+i_{ 3 })+Ri_{ 2 }=2Ri_{ 2 }+Ri_{ 3 }\)

さらに②式を代入すると

\(E=2(Ri_{ 3 }+L\frac{di_{ 3 }}{dt})+Ri_{ 3 }\)

\( =3Ri_{ 3 }+2L\frac{di_{ 3 }}{dt}\)

となり、

(1)・・・\(3R\)(ワ)

(2)・・・\(2L\)(カ)

(3),(4)の回答

(1),(2)で求めた微分方程式

\( E=3Ri_{ 3 }+2L\frac{di_{ 3 }}{dt}\)ラプラス変換する。

\( \displaystyle \frac{E}{s}＝3RI_{ 3 }(s)+2L(sI_{ 3 }(s)-i_{ 3 }(0))\)

題意より、\( i_{ 3 }(0)=0\)なので

\( \displaystyle \frac{E}{s}＝3RI_{ 3 }(s)+2sLI_{ 3 }(s)\)

\(I_{ 3 }(s)=\displaystyle \frac{E}{s}\times\displaystyle \frac{1}{3R+2sL}\)

\( I_{ 3 }(s)=\displaystyle \frac{E}{s}\times\displaystyle \frac{1}{2L}\times\displaystyle \frac{1}{s+\frac{3R}{2L}}\)

部分分数分解をすると、

\( I_{ 3 }(s)=\displaystyle \frac{E}{2L}\times（\displaystyle \frac{1}{s}ー\displaystyle \frac{1}{s+\frac{3R}{2L}}）\times\displaystyle \frac{2L}{3R}\)

\( I_{ 3 }(s)=\displaystyle \frac{E}{3R}\times（\displaystyle \frac{1}{s}ー\displaystyle \frac{1}{s+\frac{3R}{2L}}）\)

\(I_{ 3 }(s)\)を逆ラプラス変換すると

\(i_{ 3 }(t)=\displaystyle\frac{E}{3R}\times(1-e^{ -\frac{3R}{2L}t})\)

(3)・・・\(\displaystyle\frac{E}{3R}\)(イ)

(4)・・・\(\displaystyle\frac{2L}{3R}\)(ヨ)

(5)の回答

題意よりスイッチを閉じてから十分な時間が経過した場合の\(i_{ 3 }(t)\)は

\(t=\infty\)なので

\(i_{ 3 }(\infty)=\displaystyle\frac{E}{3R}\times(1-e^{ -\frac{3R}{2L}\times\infty})\)

\(i_{ 3 }(\infty)=\displaystyle\frac{E}{3R}\times(1-0)\)

\(i_{ 3 }(\infty)=\displaystyle\frac{E}{3R}\)・・・（A)となる。

次にスイッチを開けた瞬間の\(\acute{i}_{ 3 }(0)\)は上記で求めた（A)なので

\(\acute{i}_{ 3 }(0)＝i_{ 3 }(\infty)=\displaystyle\frac{E}{3R}\)

次にスイッチを開けた場合の微分方程式は

\( 0=2R\acute{i}_{ 3 }(t)+L\displaystyle\frac{d\acute{i}_{ 3 }(t)}{dt}\)

これをラプラス変換すると

\( 0=2R\acute{I}_{ 3 }(s)+L(s\acute{I}_{ 3 }(s)-\acute{i}_{ 3 }(0))\)

\(\acute{i}_{ 3 }(0)=\displaystyle\frac{E}{3R}\)なので、

\( 0=2R\acute{I}_{ 3 }(s)+L(s\acute{I}_{ 3 }(s)-\displaystyle\frac{E}{3R})\)

整理して、

\(\displaystyle\frac{EL}{3R}=(2R+sL)\acute{I}_{ 3 }(s)\)

\(\acute{I}_{ 3 }(s)=\displaystyle\frac{EL}{3R}\displaystyle\frac{1}{L}\displaystyle\frac{1}{s+\frac{2R}{L}}\)

\(\acute{I}_{ 3 }(s)=\displaystyle\frac{E}{3R}\displaystyle\displaystyle\frac{1}{s+\frac{2R}{L}}\)

これを逆ラプラス変換すると

\(\acute{i}_{ 3 }(t)=\displaystyle\frac{E}{3R}(e^{ -\frac{2R}{L}(t-T)})\)

よって答えは

(5)・・・\(\displaystyle\frac{L}{２R}\)(チ)

所感

過去問【電験二種（理論）＜R４：問４＞】過渡現象をラプラス変換で解きました。

この問題は以下の３つが重要です。

1. ラプラス変換の公式が暗記できているか
2. 部分分数分解を理解しているか
3. スイッチ開ける前後での微分方程式を立てられるか

いずれも電験二種受験者にとっては必要事項なのでしっかりと理解しておきましょう。

以上、参考になれば嬉しいです。

最後まで読んでいただき、ありがとうございました！

ゆーせい

電験一種　リベンジ

X

おはようございます！ 朝活電気エンジニアのゆーせいです。 電気系エンジニア向けの資格である電気主任技術者試験（電験）について 自身の経験に基づき情報を発信します。